Complete Question
The complete question is shown on the first uploaded image
Answer:
The 95% interval for
 is
is
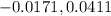
Option A is correct
Explanation:
From the question we are told that
The sample size of male is

The number of males that said they have at least one tattoo is
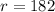
The sample size of female is

The number of females that said they have at least one tattoo is
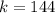
Generally the sample proportion of male is

substituting values
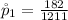
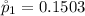
Generally the sample proportion of female is
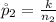
substituting values
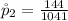
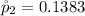
Given that the confidence level is 95% then the level of significance is mathematically represented as
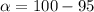
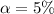

Next we obtain the critical value of
 from the normal distribution table , the value is
from the normal distribution table , the value is
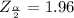
Generally the margin of error is mathematically represented as
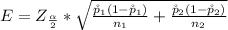
substituting values

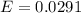
The 95% confidence interval is mathematically represented as

substituting values

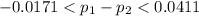
So the interpretation is that there is 95% confidence that the difference of the proportion is in the interval .So conclude that there is insufficient evidence of a significant difference in the proportion of male and female that have at least one tattoo
This because the difference in proportion is less than
