Question

A United Nations report shows the mean family income for Mexican migrants to the United States is $26,500 per year. A FLOC (Farm Labor Organizing Committee) evaluation of 24 Mexican family units reveals a mean to be $30,150 with a sample standard deviation of $10,560. State the null hypothesis and the alternate hypothesis.

Answer 1

The null hypothesis
`\mathtt{H_0 : \mu = 26500}`

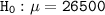
The alternative hypothesis
`\mathtt{H_1 : \mu \\eq 26500}`

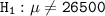
Explanation:

The summary of the given statistics is:

Population Mean = 26,500

Sample Mean = 30,150

Standard deviation = 10560

sample size = 24

The objective is to state the null hypothesis and the alternate hypothesis.

An hypothesis is a claim with insufficient information which tends to be challenged into further testing and experimentation in order to determine if such claim is significant or not.

The null hypothesis is a default hypothesis where there is no statistical significance between the two variables in the hypothesis.

The alternative hypothesis is the research hypothesis that the researcher is trying to prove.

The null hypothesis
`\mathtt{H_0 : \mu = 26500}`

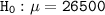
The alternative hypothesis
`\mathtt{H_1 : \mu \\eq 26500}`

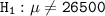
The test statistic can be computed as follows:

`z = (\overline X - \mu)/((\sigma)/(√(n)))`

`z = (30150 - 26500)/((10560)/(√(24)))`

`z = (3650)/((10560)/(4.8989))`

`z = \frac{3650 * 4.8989 }{{10560}}`

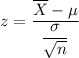
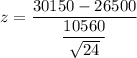
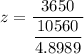
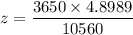
z = 1.6933