Question

6 points are place on the line a, 4 points are placed on the line b. How many triangles is it possible to form such that their verticies will be the given points, if a ∥b?

Answer 1

Answer: 96

Explanation:

Ok, lines a and b are parallel.

We can separate this problem in two cases:

Case 1: 2 vertex in line a, and one vertex in line b.

Here we use the relation:

"In a group of N elements, the total combinations of sets of K elements is given by"

`C = (N!)/((N - K)!*K!)`

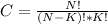
Here, the total number of points in the line is N, and K is the ones that we select to make the vertices of the triangle.

Then if we have two vertices in line a, we have:

N = 6, K = 2

`C = (6!)/(4!*2!) = (6*5)/(2) = 3*5 = 15`

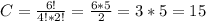
And the other vertex can be on any of the four points on the line b, so the total number of triangles is:

C = 15*4 = 60.

But we still have the case 2, where we have 2 vertices on line b, and one on line a.

First, the combination for the two vertices in line b is:

We use N = 4 and K = 2.

`C = (4!)/(2!*2!) = (4*3)/(2) = 6`

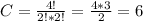
And the other vertice of the triangle can be on any of the 6 points in line a, so the total number of triangles that we can make in this case is:

C = 6*6 = 36

Then, putting together the two cases, we have a total of:

60 + 36 = 96 different triangles