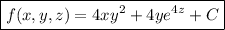Question

EXAMPLE 5 If F(x, y, z) = 4y2i + (8xy + 4e4z)j + 16ye4zk, find a function f such that ∇f = F. SOLUTION If there is such a function f, then

Answer 1

If there is such a scalar function f, then

`(\partial f)/(\partial x)=4y^2`

`(\partial f)/(\partial y)=8xy+4e^(4z)`

`(\partial f)/(\partial z)=16ye^(4z)`

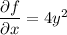
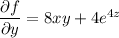
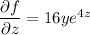
Integrate both sides of the first equation with respect to x :

`f(x,y,z)=4xy^2+g(y,z)`

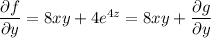
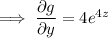
Differentiate both sides with respect to y :

`(\partial f)/(\partial y)=8xy+4e^(4z)=8xy+(\partial g)/(\partial y)`

`\implies(\partial g)/(\partial y)=4e^(4z)`

Integrate both sides with respect to y :

`g(y,z)=4ye^(4z)+h(z)`

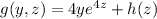
Plug this into the equation above with f , then differentiate both sides with respect to z :

`f(x,y,z)=4xy^2+4ye^(4z)+h(z)`

`(\partial f)/(\partial z)=16ye^(4z)=16ye^(4z)+(\mathrm dh)/(\mathrm dz)`

`\implies(\mathrm dh)/(\mathrm dz)=0`

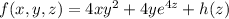
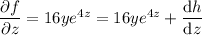
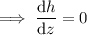
Integrate both sides with respect to z :

`h(z)=C`

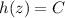
So we end up with

`\boxed{f(x,y,z)=4xy^2+4ye^(4z)+C}`