Answer: A) 1716 B) 1235520
Explanation:
- If order doesn't matter , then we use combinations, where the number of combinations of selecting r things from n is given by :-
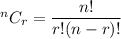
- If order matters , then we use permutations, where the number of permutations of selecting r things from n is given by :-
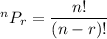
Given, Total distinct letters = 13
To choose = 6 letters
A) Number of ways to choose (if order does not matter)=
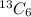
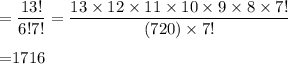
B) Number of ways to choose (if order matters)=

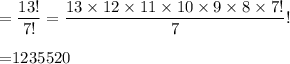
Hence, A) 1716 B) 1235520