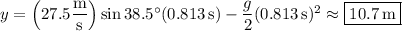The ball's horizontal position in the air is
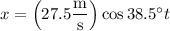
It hits the wall when
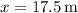 , which happens at
, which happens at
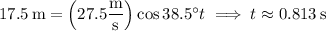
Meanwhile, the ball's vertical position is
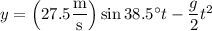
where
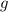 is the acceleration due to gravity, 9.80 m/s^2.
is the acceleration due to gravity, 9.80 m/s^2.
At the time the ball hits the wall, its vertical position (relative to its initial position) is