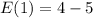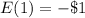Answer:
The expectation is
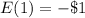
Explanation:
From the question we are told that
The first offer is
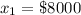
The second offer is
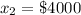
The third offer is
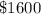
The number of tickets is
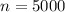
The price of each ticket is
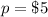
Generally expectation is mathematically represented as

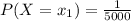 given that they just offer one
given that they just offer one
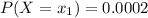
Now
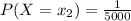 given that they just offer one
given that they just offer one
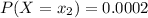
Now
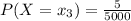 given that they offer five
given that they offer five
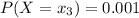
Hence the expectation is evaluated as
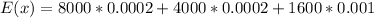
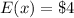
Now given that the price for a ticket is
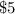
The actual expectation when price of ticket has been removed is