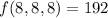Question

Use Lagrange multipliers to minimize the function subject to the following two constraints. Assume that x, y, and z are nonnegative. Question 18 options: a) 192 b) 384 c) 576 d) 128 e) 64

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

Option C is the correct option

Explanation:

From the question we are told that

The equation is
`f (x, y , z ) = x^2 +y^2 + z^2`

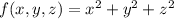
The constraint is
`P(x, y , z) = x + y + z - 24 = 0`

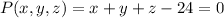
Now using Lagrange multipliers we have that

`\lambda = ( \delta f )/( \delta x ) = 2 x`

`\lambda = ( \delta f )/( \delta y ) = y`

`\lambda = ( \delta f )/( \delta z ) = 2 z`

=>
`x = ( \lambda )/(2)`

`y = ( \lambda )/(2)`

`z = ( \lambda )/(2)`

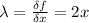
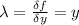
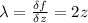
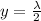
From the constraint we have

`(\lambda )/(2) + (\lambda )/(2) + (\lambda )/(2) = 24`

=>
`(3 \lambda )/(2) = 24`

=>
`\lambda = 16`

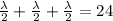
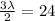
substituting for x, y, z

=> x = 8

=> y = 8

=> z = 8

Hence

`f (8, 8 , 8 ) = 8^2 +8^2 + 8^2`

`f (8, 8 , 8 ) = 192`