Answer:
The test statistic for testing if the proportion of high-altitude vehicles exceeding the standard is greater than the proportion of low-altitude vehicles exceeding the standard is 3.234.
Explanation:
We are given that in a random sample of 380 cars driven at low altitudes, 42 of them exceeded a standard of 10 grams of particulate pollution per gallon of fuel consumed.
In an independent random sample of 90 cars driven at high altitudes, 24 of them exceeded the standard.
Let
 = population proportion of cars driven at high altitudes who exceeded a standard of 10 grams.
= population proportion of cars driven at high altitudes who exceeded a standard of 10 grams.
 = population proportion of cars driven at low altitudes who exceeded a standard of 10 grams.
= population proportion of cars driven at low altitudes who exceeded a standard of 10 grams.
So, Null Hypothesis,
 :
:
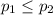 {means that the proportion of high-altitude vehicles exceeding the standard is smaller than or equal to the proportion of low-altitude vehicles exceeding the standard}
{means that the proportion of high-altitude vehicles exceeding the standard is smaller than or equal to the proportion of low-altitude vehicles exceeding the standard}
Alternate Hypothesis,
 :
:
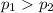 {means that the proportion of high-altitude vehicles exceeding the standard is greater than the proportion of low-altitude vehicles exceeding the standard}
{means that the proportion of high-altitude vehicles exceeding the standard is greater than the proportion of low-altitude vehicles exceeding the standard}
The test statistics that will be used here is Two-sample z-test statistics for proportions;
T.S. =
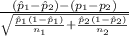 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of cars driven at high altitudes who exceeded a standard of 10 grams =
= sample proportion of cars driven at high altitudes who exceeded a standard of 10 grams =
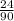 = 0.27
= 0.27
 = sample proportion of cars driven at low altitudes who exceeded a standard of 10 grams =
= sample proportion of cars driven at low altitudes who exceeded a standard of 10 grams =
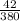 = 0.11
= 0.11
 = sample of cars driven at high altitudes = 90
= sample of cars driven at high altitudes = 90
 = sample of cars driven at low altitudes = 380
= sample of cars driven at low altitudes = 380
So, the test statistics =
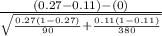
= 3.234
The value of z-test statistics is 3.234.