Answer:
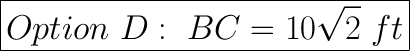
Explanation:
Since it's a right angled triangle, We'll use trigonometric rations.
Given that m∠B = 45°
So,
Sin B = opposite / hypotenuse
Where m∠B = 45°, opposite = 10 ft and hypotenuse = BC
Sin 45 = 10 / BC
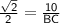
BC = 20 / √2
Multiplying and Dividing by √2
BC = 20√2 / √(2)²
BC = 20 √2 / 2
BC = 10√2 ft