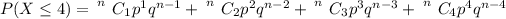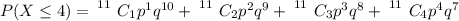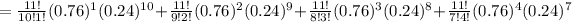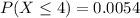Question

At an airport, 76% of recent flights have arrived on time. A sample of 11 flights is studied. Find the probability that no more than 4 of them were on time.

Answer 1

The probability is
`P( X \le 4 ) = 0.0054`

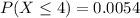
Explanation:

From the question we are told that

The percentage that are on time is p = 0.76

The sample size is n = 11

Generally the percentage that are not on time is

`q = 1- p`

`q = 1- 0.76`

`q = 0.24`

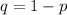
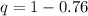
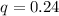
The probability that no more than 4 of them were on time is mathematically represented as

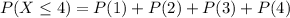
`P( X \le 4 ) = P(1 ) + P(2) + P(3) + P(4)`

=>
`P( X \le 4 ) = \left n } \atop {}} \right.C_1 p^(1) q^(n- 1) + \left n } \atop {}} \right.C_2p^(2) q^(n- 2) + \left n } \atop {}} \right.C_3 p^(3) q^(n- 3) + \left n } \atop {}} \right.C_4 p^(4) q^(n- 4)`

`P( X \le 4 ) = \left 11 } \atop {}} \right.C_1 p^(1) q^(11- 1) + \left 11 } \atop {}} \right.C_2p^(2) q^(11- 2) + \left 11 } \atop {}} \right.C_3 p^(3) q^(11- 3) + \left 11 } \atop {}} \right.C_4 p^(4) q^(11- 4)`

`P( X \le 4 ) = \left 11 } \atop {}} \right.C_1 p^(1) q^(10) + \left 11 } \atop {}} \right.C_2p^(2) q^(9) + \left 11 } \atop {}} \right.C_3 p^(3) q^(8) + \left 11 } \atop {}} \right.C_4 p^(4) q^(7)`

`= (11! )/( 10! 1!) (0.76)^(1) (0.24)^(10) + (11!)/(9! 2!) (0.76)^2 (0.24)^(9) + (11!)/(8! 3!) (0.76)^(3) (0.24)^(8) + (11!)/(7!4!) (0.76)^(4) (0.24)^(7)`

`P( X \le 4 ) = 0.0054`