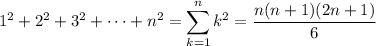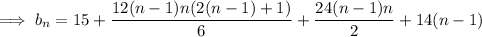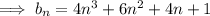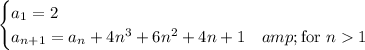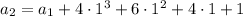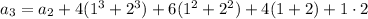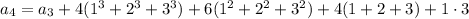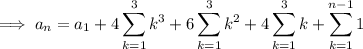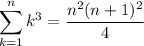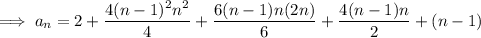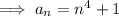Question

2,17,82,257,626,1297 next one please ?​

Answer 1

The easy thing to do is notice that 1^4 = 1, 2^4 = 16, 3^4 = 81, and so on, so the sequence follows the rule
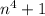`n^4+1`. The next number would then be fourth power of 7 plus 1, or 2402.

And the harder way: Denote the n-th term in this sequence by
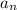`a_n`, and denote the given sequence by
`\{a_n\}_(n\ge1)`.

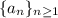Let
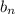`b_n` denote the n-th term in the sequence of forward differences of
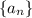`\{a_n\}`, defined by

`b_n=a_(n+1)-a_n`

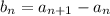
for n ≥ 1. That is,
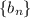`\{b_n\}` is the sequence with

`b_1=a_2-a_1=17-2=15`

`b_2=a_3-a_2=82-17=65`

`b_3=a_4-a_3=175`

`b_4=a_5-a_4=369`

`b_5=a_6-a_5=671`

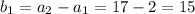
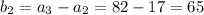
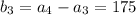
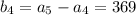
and so on.

Next, let
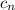`c_n` denote the n-th term of the differences of
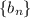`\{b_n\}`, i.e. for n ≥ 1,

`c_n=b_(n+1)-b_n`

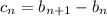
so that

`c_1=b_2-b_1=65-15=50`

`c_2=110`

`c_3=194`

`c_4=302`

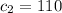
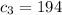
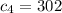
etc.

Again: let
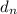`d_n` denote the n-th difference of
`\{c_n\}`:

`d_n=c_(n+1)-c_n`

`d_1=c_2-c_1=60`

`d_2=84`

`d_3=108`

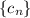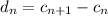
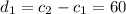
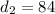
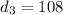
etc.

One more time: let
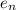`e_n` denote the n-th difference of
`\{d_n\}`:

`e_n=d_(n+1)-d_n`

`e_1=d_2-d_1=24`

`e_2=24`

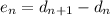
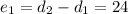
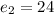
etc.

The fact that these last differences are constant is a good sign that
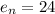`e_n=24` for all n ≥ 1. Assuming this, we would see that
`\{d_n\}` is an arithmetic sequence given recursively by

`\begin{cases}d_1=60\\d_(n+1)=d_n+24&\text{for }n>1\end{cases}`

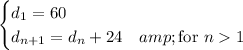
and we can easily find the explicit rule:

`d_2=d_1+24`

`d_3=d_2+24=d_1+24\cdot2`

`d_4=d_3+24=d_1+24\cdot3`

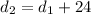
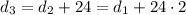
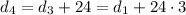
and so on, up to

`d_n=d_1+24(n-1)`

`d_n=24n+36`

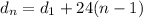
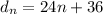
Use the same strategy to find a closed form for
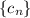`\{c_n\}`, then for
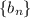`\{b_n\}`, and finally
`\{a_n\}`.

`\begin{cases}c_1=50\\c_(n+1)=c_n+24n+36&\text{for }n>1\end{cases}`

`c_2=c_1+24\cdot1+36`

`c_3=c_2+24\cdot2+36=c_1+24(1+2)+36\cdot2`

`c_4=c_3+24\cdot3+36=c_1+24(1+2+3)+36\cdot3`

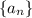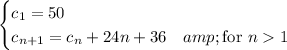
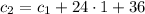
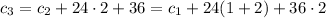
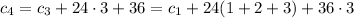
and so on, up to

`c_n=c_1+24(1+2+3+\cdots+(n-1))+36(n-1)`

Recall the formula for the sum of consecutive integers:

`1+2+3+\cdots+n=\displaystyle\sum_(k=1)^nk=\frac{n(n+1)}2`

`\implies c_n=c_1+\frac{24(n-1)n}2+36(n-1)`

`\implies c_n=12n^2+24n+14`

`\begin{cases}b_1=15\\b_(n+1)=b_n+12n^2+24n+14&\text{for }n>1\end{cases}`

`b_2=b_1+12\cdot1^2+24\cdot1+14`

`b_3=b_2+12\cdot2^2+24\cdot2+14=b_1+12(1^2+2^2)+24(1+2)+14\cdot2`

`b_4=b_3+12\cdot3^2+24\cdot3+14=b_1+12(1^2+2^2+3^2)+24(1+2+3)+14\cdot3`

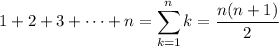
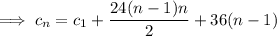
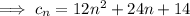
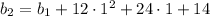
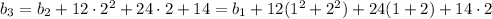
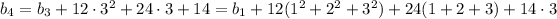
and so on, up to

`b_n=b_1+12(1^2+2^2+3^2+\cdots+(n-1)^2)+24(1+2+3+\cdots+(n-1))+14(n-1)`

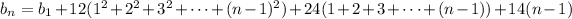
Recall the formula for the sum of squares of consecutive integers:

`1^2+2^2+3^2+\cdots+n^2=\displaystyle\sum_(k=1)^nk^2=\frac{n(n+1)(2n+1)}6`

`\implies b_n=15+\frac{12(n-1)n(2(n-1)+1)}6+\frac{24(n-1)n}2+14(n-1)`

`\implies b_n=4n^3+6n^2+4n+1`

`\begin{cases}a_1=2\\a_(n+1)=a_n+4n^3+6n^2+4n+1&\text{for }n>1\end{cases}`

`a_2=a_1+4\cdot1^3+6\cdot1^2+4\cdot1+1`

`a_3=a_2+4(1^3+2^3)+6(1^2+2^2)+4(1+2)+1\cdot2`

`a_4=a_3+4(1^3+2^3+3^3)+6(1^2+2^2+3^2)+4(1+2+3)+1\cdot3`

`\implies a_n=a_1+4\displaystyle\sum_(k=1)^3k^3+6\sum_(k=1)^3k^2+4\sum_(k=1)^3k+\sum_(k=1)^(n-1)1`

`\displaystyle\sum_(k=1)^nk^3=\frac{n^2(n+1)^2}4`

`\implies a_n=2+\frac{4(n-1)^2n^2}4+\frac{6(n-1)n(2n)}6+\frac{4(n-1)n}2+(n-1)`

`\implies a_n=n^4+1`