Question

Suppose that X; Y have constant joint density on the triangle with corners at (4; 0), (0; 4), and the origin. a) Find P(X < 3; Y < 3). b) Are X and Y independent

Answer 1

The triangle (call it T ) has base and height 4, so its area is 1/2*4*4 = 8. Then the joint density function is

`f_(X,Y)(x,y)=\begin{cases}\frac18&\text{for }(x,y)\in T\\0&\text{otherwise}\end{cases}`

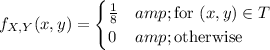
where T is the set

`T=\{(x,y)\mid 0\le x\le4\land0\le y\le4-x\}`

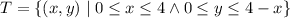
(a) I've attached an image of the integration region.

`P(X<3,Y<3)=\displaystyle\int_0^1\int_0^3f_(X,Y)(x,y)\,\mathrm dy\,\mathrm dx+\int_1^3\int_0^(4-x)f_(X,Y)(x,y)\,\mathrm dy\,\mathrm dx=\frac12`

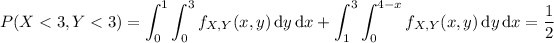
(b) X and Y are independent if the joint distribution is equal to the product of their marginal distributions.

Get the marginal distributions of one random variable by integrating the joint density over all values of the other variable:

`f_X(x)=\displaystyle\int_(-\infty)^\infty f_(X,Y)(x,y)\,\mathrm dy=\int_0^(4-x)\frac{\mathrm dy}8=\begin{cases}\frac{4-x}8&\text{for }0\le x\le4\\0&\text{otherwise}\end{cases}`

`f_Y(y)=\displaystyle\int_(-\infty)^\infty f_(X,Y)(x,y)\,\mathrm dx=\int_0^(4-y)\frac{\mathrm dx}8=\begin{cases}\frac{4-y}8&\text{for }0\le y\le4\\0&\text{otherwise}\end{cases}`

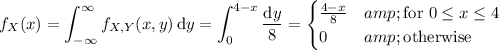
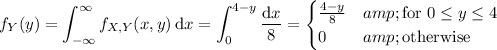
Clearly,
`f_(X,Y)(x,y)\\eq f_X(x)f_Y(y)`, so they are not independent.