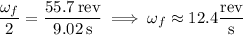(a) The car is undergoing an acceleration of
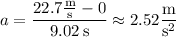
so that in 9.02 s, it will have covered a distance of
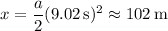
The car has tires with diameter d = 58.5 cm = 0.585 m, and hence circumference π d ≈ 1.84 m. Divide the distance traveled by the tire circumference to determine how many revolutions it makes:
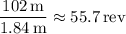
(b) The wheels have average angular velocity
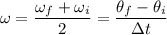
where
 is the average angular velocity,
is the average angular velocity,
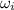 and
and
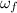 are the initial and final angular velocities (rev/s),
are the initial and final angular velocities (rev/s),
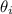 and
and
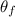 are the initial and final angular displacements (rev), respectively, and
are the initial and final angular displacements (rev), respectively, and
 is the duration of the time between initial and final measurements. The second equality holds because acceleration is constant.
is the duration of the time between initial and final measurements. The second equality holds because acceleration is constant.
The wheels start at rest, so