Question

Consider a pair of random variables X; Y with constant joint density on the quadrilateral with vertices (0; 0), (2; 0), (2; 6), (0; 12). a) Find the expected value E(X). b) Find the expected value E(Y ).

Answer 1

The given quadrilateral (call it Q) is a trapezoid with "base" lengths of 6 and 12, and "height" 2, so its area is (6 + 12)/2*2 = 18. This means the joint density is

`f_(X,Y)(x,y)=\begin{cases}\frac1{18}&\text{for }(x,y)\in Q\\0&\text{otherwise}\end{cases}`

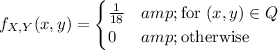
where Q is the set of points

`Q=\{(x,y)\mid0\le x\le 2\land0\le y\le12-3x\}`

(y = 12 - 3x is the equation of the line through the points (0, 12) and (2, 6))

Recall the definition of expectation:

`E[g(X,Y)]=\displaystyle\int_(-\infty)^\infty\int_(-\infty)^\infty g(x,y)f_(X,Y)(x,y)\,\mathrm dx\,\mathrm dy`

(a) Using the definition above, we have

`E[X]=\displaystyle\int_(-\infty)^\infty\int_(-\infty)^\infty xf_(X,Y)(x,y)\,\mathrm dx\,\mathrm dy=\int_0^2\int_0^(12-3x)\frac x{18}\,\mathrm dy\,\mathrm dx=\frac89`

(b) Likewise,

`E[Y]=\displaystyle\int_(-\infty)^\infty\int_(-\infty)^\ifnty yf_(X,Y)(x,y)\,\mathrm dx\,\mathrm dy=\int_0^2\int_0^(12-3x)\frac y{18}\,\mathrm dy\,\mathrm dx=\frac{14}3`