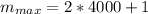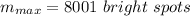Question

Given a double slit apparatus with slit distance 2 mm, what is the theoretical maximum number of bright spots that I would see when I shine light with a wavelength 500 nm on the slits

Answer 1

The values is
`m_(max) = 8001 \ bright \ spots`

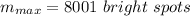
Step-by-step explanation:

From the question we are told that

The slit distance is
`d = 2 \ mm = 2*10^(-3) \ m`

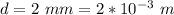
The wavelength is
`\lambda = 500 \ nm = 500 *10^(-9) \ m`

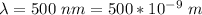
At the first half of the screen from the central maxima

The number of bright spot according to the condition for constructive interference is

`n = (d * sin (\theta ))/(\lambda)`

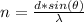
For maximum number of spot
`\theta = 90^o`

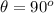
So

`n = (2*10^(-3) * sin (90 ))/(500 *10^(-9))`

`n =4000`

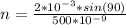
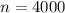
Now for the both sides plus the central maxima we have

`m_(max) = 2 * n + 1`

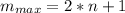
substituting values

`m_(max) = 2 * 4000 + 1`

`m_(max) = 8001 \ bright \ spots`