Question

Pls find the answer for question 2

Answer 1

The answer is C. 0

Explanation:

since

`(x)/(y) + (y)/(x ) = - 1`

we multiply both sides by xy to cancel their denominators and multiply -1 by xy

so we have

`xy( (x)/(y)) + xy( (x)/(y) ) = xy * - 1`

we get our answer as

`{x}^(2) + {y}^(2) = - xy`

we were given the difference of cubes that is

`{x}^(3) - {y}^(3)`

which is =

`(x - y)( {x}^(2) + xy + {y}^(2) )`

so since,

`{x}^(2) + {y}^(2) = - xy`

we substitute,

`(x - y)( - xy + xy) = (x - y)(0) = 0`

Answer 2

c

Explanation:

x³ - y³ ← is a difference of cubes and factors as

x³ - y³ = (x - y)(x² + xy + y²)

Given

`(x)/(y)` +
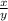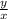`(y)/(x)` = - 1

Multiply through by xy to clear the fractions

x² + y² = - xy ← substitute into second factor of expansion

x³ - y³ = (x - y)(- xy + xy) = (x - y) × 0 = 0 → c