Answer:
The 95% confidence interval is

Explanation:
From the question we are told that
The sample mean for fat-blocking
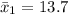
The sample size for fat-blocking

The standard deviation for fat-blocking is

The sample mean for control group is
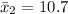
The sample size for control group is
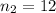
The standard deviation for control group is

Given that the confidence level is 95% then the level of significance can me mathematically evaluated as
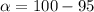


Generally the degree of freedom is mathematically represented as
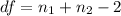
substituting values
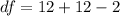
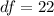
Next we obtain the critical value of
 at a degree of freedom of 22 form the students t-distribution , the value is
at a degree of freedom of 22 form the students t-distribution , the value is
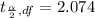
Generally the margin of error is mathematically represented as

substituting values


the 95% confidence interval for the differences of the means is mathematically represented as

substituting values

