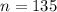Answer:
The sample required is
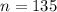
Explanation:
From the question we are told that
The standard deviation is
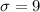
The margin of error is

Given that the confidence level is 99% then the level of significance is mathematically evaluated as
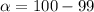


Next we will obtain the critical value
 from the normal distribution table(reference math dot armstrong dot edu) , the value is
from the normal distribution table(reference math dot armstrong dot edu) , the value is
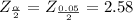
The sample size is mathematically represented as
![n = [ \frac{Z_{(\alpha )/(2) } * \sigma }{E} ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/vwv2odauclk6lmr9vfh7htl4qx2fjlkg6i.png)
substituting values
![n = [ ( 2.58 * 9 )/(2) ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/6ltqlo2lmzedw805pfy2pdlp626sf54gnt.png)