Question

A certain​ animal's body temperature has a mean of F and a standard deviation of F. Convert the given temperatures to z scores.

Answer 1

A certain​ animal's body temperature has a mean of 94.72° F and a standard deviation of 0.57°F. Convert the given temperatures to z scores.

a. 93.52 °F b. 95.22 °F c. 94.72 °F

Answer:

a. z = - 2.1053

b. z = 0.87719

c. z = 0

Explanation:

Given that :

The population mean μ = 94.72

The standard deviation σ = 0.57

the formula for calculating the standard normal z score, which can be represented as:

`z= (\overline x - \mu)/(\sigma)`

For a.

The sample mean
`\bar x` = 93.52

The z score can be computed as follows:

`z= (\overline x - \mu)/(\sigma)`

`z= (93.52 - 94.72)/(0.57)`

`z= (-1.2)/(0.57)`

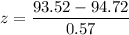
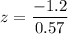
z = - 2.1053

For b.

The sample mean
`\bar x` = 95.22

`z= (\overline x - \mu)/(\sigma)`

`z= (95.22 - 94.72)/(0.57)`

`z= (0.5)/(0.57)`

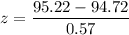
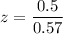
z = 0.87719

For c.

The sample mean
`\bar x` = 94.72

`z= (\overline x - \mu)/(\sigma)`

`z= (94.72 - 94.72)/(0.57)`

`z= (0)/(0.57)`

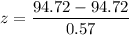
z = 0