Question

Maria and Nate graphed lines on a coordinate plane. Maria's line is represented by the equation y = -5/6x +8. Nate's line is perpendicular to Maria's line. Which of the following could be an equation for Nate's line?

a 5x-6y=15
b 5x+6y=15
c 6x-5y=15
d 6x+5y=15

Answer 1

c) 6x - 5y = 15

Explanation:

Slope-intercept form of a linear equation:
`y=mx+b`

(where m is the slope and b is the y-intercept)

Maria's line:
`y=-(5)/(6)x+8`

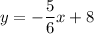
Therefore, the slope of Maria's line is
`-(5)/(6)`

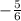
If two lines are perpendicular to each other, the product of their slopes will be -1.

Therefore, the slope of Nate's line (m) is:

`\begin{aligned}\implies m * -(5)/(6) &=-1\\m & =(6)/(5)\end{aligned}`

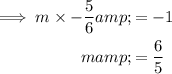
Therefore, the linear equation of Nate's line is:

`y=(6)/(5)x+b\quad\textsf{(where b is some constant)}`

Rearranging this to standard form:

`\implies y=(6)/(5)x+b`

`\implies 5y=6x+5b`

`\implies 6x-5y=-5b`

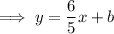
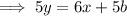
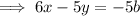
Therefore, option c could be an equation for Nate's line.