Question

I NEED HELP ASAP

191 of the 288 high school students surveyed at a local school said they went outside more during school hours as elementary school students than they do now as high school students. Calculate the Margin of Error, rounded to the nearest tenth of a percent. Is it reasonable that the state education department claims the percentage for the entire state is 73%? Justify your answer.

Answer 1

It is not reasonable that the state education department claims the percentage for the entire state is 73%.

Explanation:

We are given that 191 of the 288 high school students surveyed at a local school said they went outside more during school hours as elementary school students than they do now as high school students.

Firstly, the pivotal quantity for finding the confidence interval for the population proportion is given by;

P.Q. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of high school students who went outside more during school hours as elementary school students than they do now as high school students =
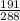`(191)/(288)` = 0.66

n = sample of high school students = 288

p = population percentage for the entire state

Here for constructing a 90% confidence interval we have used a One-sample z-test for proportions.

The margin of error is given by;

M.E. =
`2 * \sqrt{(\hat p(1-\hat p))/(n) }`

=
`2 * \sqrt{(0.66(1-0.66))/(288) }`

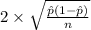
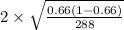
M.E. = 0.056 or 5.6%

So, the confidence interval so formed =
`\hat p \pm \text{Margin of error}`

= [
`0.66 - 0.056 , 0.66 + 0.056`]

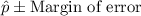
= [0.604, 0.716]

Since the above interval does not include 0.73 or the population proportion of 73% falls outside the above interval. So, it is not reasonable that the state education department claims the percentage for the entire state is 73%.