Question

What are the vertical and horizontal asymptotes for the function f(x)=
3x2/x2-4

Answer 1

Answer: f(x) will have vertical asymptotes at x=-2 and x=2 and horizontal asymptote at y=3.

Explanation:

Given function:
`f(x)=(3x^2)/(x^2-4)`

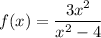
The vertical asymptote occurs for those values of x which make function indeterminate or denominator 0.

i.e.
`x^2-4=0\Rightarrow\ x^2=4\Rightarrow\ x=\pm2`

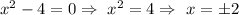
Hence, f(x) will have vertical asymptotes at x=-2 and x=2.

To find the horizontal asymptote , we can see that the degree of numerator and denominator is same i.e. 2.

So, the graph will horizontal asymptote at
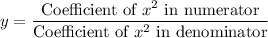
`y=\frac{\text{Coefficient of }x^2\text{ in numerator}}{\text{Coefficient of }x^2\text{ in denominator}}`

i.e.
`y=(3)/(1)=3`

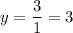
Hence, f(x) will have horizontal asymptote at y=3.