Question

Joy is preparing 20 liters of a 25% saline solution. She has only a 40% solution and a 10% solution in her lab. How many liters of the 40% solution and how many liters of the 10% solution should she mix to make the 25% solution?

Answer 1

10 Liters of 40% solution

Explanation:

Answer 2

10 liters of the 40% solution, and 10 liters of the 10% solution

Explanation:

Let us say that x = the liters of the 40% solution, and y = liters of the 10% solution in her lab. We know that Joy is preparing a solution containing a total 20 liters, so x + y = 20. We can respectively create the following system of equations,

x + y = 20,

0.40x + 0.10y = 0.25 ( 20 )

And now we have to solve this system of equations for x and y, the liters of the 40% solution and the liters of the 10% solution,

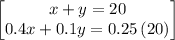`\begin{bmatrix}x+y=20\\ 0.4x+0.1y=0.25\left(20\right)\end{bmatrix}` ( Substitute x as 20 - y )

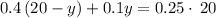`0.4\left(20-y\right)+0.1y=0.25\cdot \:20\end{bmatrix}` ( Isolate y )

`8-0.3y=5` ⇒
`80-3y=50` ⇒
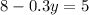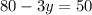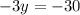`-3y=-30` ⇒ y = 10

`x=20-10 = 10` ⇒ x = 10

Therefore, there are 10 liters of both the 40% and 10% solution.