Question

A surveyor wants to find the height of a hill. He determines that the angle of elevation to the top of the hill is 50°. He then walks 40

feet farther from the base from the hill and determines that the angle of elevation to the top of the hill is now 30°. Find the height of
the hill (round to the nearest foot).
es

Answer 1

The answer is 45 feet

Answer 2

The height of the hill is 45 feet .

Explanation:

Refer the attached figure

Let AB be the height of hill

We are given that He determines that the angle of elevation to the top of the hill is 50°

So,
`\angle ACB= 50^(\circ)`

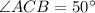
Now He then walks 40 feet farther from the base from the hill and determines that the angle of elevation to the top of the hill is now 30°

So, CD=40 feet

BD=BC+CD=BC+40

`\ADB= 30^(\circ)`

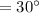
In ΔACB

`Tan \theta = (Perpendicular)/(Base)\\Tan 50^(\circ) =(AB)/(BC)\\1.1917 BC=AB ----1`

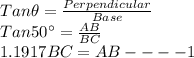
In ΔADB

`Tan \theta = (Perpendicular)/(Base)\\Tan 30^(\circ) =(AB)/(BD)\\(1)/(√(3))=(AB)/(BC+40)\\(1)/(√(3))(BC+40)=AB----2`

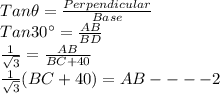
So,equate 1 and 2

`1.1917 BC=(1)/(√(3))(BC+40)\\BC=37.59`

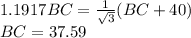
Substitute the value in equation 1

1.1917 (37.59)=AB

44.796=AB

Hence the height of the hill is 45 feet .