Question

Find the fourth roots of 16(cos 200° + i sin 200°).

Answer 1

See below.

Explanation:

To find roots of an equation, we use this formula:

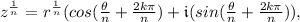`z^{(1)/(n)}=r^{(1)/(n)}(cos((\theta)/(n)+(2k\pi)/(n) )+\mathfrak{i}(sin((\theta)/(n)+(2k\pi)/(n))),` where k = 0, 1, 2, 3... (n = root; equal to n - 1; dependent on the amount of roots needed - 0 is included).

In this case, n = 4.

Therefore, we adjust the polar equation we are given and modify it to be solved for the roots.

Part 2: Solving for root #1

To solve for root #1, make k = 0 and substitute all values into the equation. On the second step, convert the measure in degrees to the measure in radians by multiplying the degrees measurement by
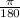`(\pi)/(180)` and simplify.

`z^{(1)/(4)}=16^{(1)/(4)}(cos((200)/(4)+(2(0)\pi)/(4)))+\mathfrak{i}(sin((200)/(4)+(2(0)\pi)/(4)))`

`z^{(1)/(4)}=2(cos((5\pi)/(18)+(\pi)/(4)))+\mathfrak{i}(sin((5\pi)/(18)+(\pi)/(4)))`

`z^{(1)/(4)} = 2(sin((5\pi)/(18)+(\pi)/(4)))+\mathfrak{i}(sin((5\pi)/(18)+(\pi)/(4)))`

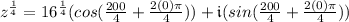
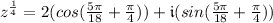
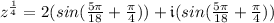
Root #1:

`\large\boxed{z^(1)/(4)=2(cos((19\pi)/(36)))+\mathfrack{i}(sin((19\pi)/(38)))}`

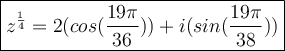
Part 3: Solving for root #2

To solve for root #2, follow the same simplifying steps above but change k to k = 1.

`z^{(1)/(4)}=16^{(1)/(4)}(cos((200)/(4)+(2(1)\pi)/(4)))+\mathfrak{i}(sin((200)/(4)+(2(1)\pi)/(4)))`

`z^{(1)/(4)}=2(cos((5\pi)/(18)+(2\pi)/(4)))+\mathfrak{i}(sin((5\pi)/(18)+(2\pi)/(4)))\\`

`z^{(1)/(4)}=2(cos((5\pi)/(18)+(\pi)/(2)))+\mathfrak{i}(sin((5\pi)/(18)+(\pi)/(2)))\\`

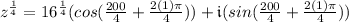
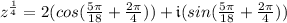
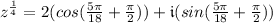
Root #2:

`\large\boxed{z^{(1)/(4)}=2(cos((7\pi)/(9)))+\mathfrak{i}(sin((7\pi)/(9)))}`

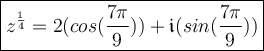
Part 4: Solving for root #3

To solve for root #3, follow the same simplifying steps above but change k to k = 2.

`z^{(1)/(4)}=16^{(1)/(4)}(cos((200)/(4)+(2(2)\pi)/(4)))+\mathfrak{i}(sin((200)/(4)+(2(2)\pi)/(4)))`

`z^{(1)/(4)}=2(cos((5\pi)/(18)+(4\pi)/(4)))+\mathfrak{i}(sin((5\pi)/(18)+(4\pi)/(4)))\\`

`z^{(1)/(4)}=2(cos((5\pi)/(18)+\pi))+\mathfrak{i}(sin((5\pi)/(18)+\pi))\\`

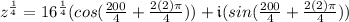
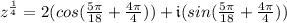
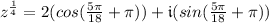
Root #3:

`\large\boxed{z^{(1)/(4)}=2(cos((23\pi)/(18)))+\mathfrak{i}(sin((23\pi)/(18)))}`

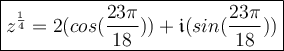
Part 4: Solving for root #4

To solve for root #4, follow the same simplifying steps above but change k to k = 3.

`z^{(1)/(4)}=16^{(1)/(4)}(cos((200)/(4)+(2(3)\pi)/(4)))+\mathfrak{i}(sin((200)/(4)+(2(3)\pi)/(4)))`

`z^{(1)/(4)}=2(cos((5\pi)/(18)+(6\pi)/(4)))+\mathfrak{i}(sin((5\pi)/(18)+(6\pi)/(4)))\\`

`z^{(1)/(4)}=2(cos((5\pi)/(18)+(3\pi)/(2)))+\mathfrak{i}(sin((5\pi)/(18)+(3\pi)/(2)))\\`

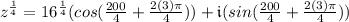
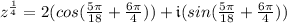
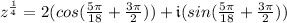
Root #4:

`\large\boxed{z^{(1)/(4)}=2(cos((16\pi)/(9)))+\mathfrak{i}(sin((16\pi)/(19)))}`

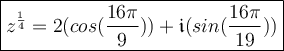
The fourth roots of 16(cos 200° + i(sin 200°) are listed above.