Answer:
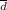 = −0.26
= −0.26
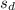 = 0.4219
= 0.4219
Explanation:
Given:
Sample1: 98.1 98.8 97.3 97.5 97.9
Sample2: 98.7 99.4 97.7 97.1 98.0
Sample 1 Sample 2 Difference d
98.1 98.7 -0.6
98.8 99.4 -0.6
97.3 97.7 -0.4
97.5 97.1 0.4
97.9 98.0 -0.1
To find:
Find the values of
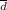 and
and
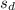
d overbar (
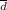 ) is the sample mean of the differences which is calculated by dividing the sum of all the values of difference d with the number of values i.e. n = 5
) is the sample mean of the differences which is calculated by dividing the sum of all the values of difference d with the number of values i.e. n = 5
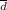 = ∑d/n
= ∑d/n
= (−0.6 −0.6 −0.4 +0.4 −0.1) / 5
= −1.3 / 5
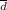 = −0.26
= −0.26
s Subscript d is the sample standard deviation of the difference which is calculated as following:
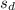 = √∑(
= √∑(
 -
-
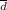 )²/ n-1
)²/ n-1
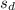 =
=
√
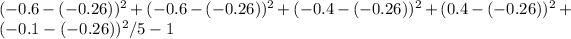
= √ (−0.6 − (−0.26 ))² + (−0.6 − (−0.26))² + (−0.4 − (−0.26))² + (0.4 −
(−0.26))² + (−0.1 − (−0.26))² / 5−1
=

=

=
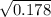
= 0.4219
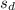 = 0.4219
= 0.4219
Subscript d represent
μ
 represents the mean of differences in body temperatures measured at 8 AM and at 12 AM of population.
represents the mean of differences in body temperatures measured at 8 AM and at 12 AM of population.