Question

A certain dataset of systolic blood pressure measurements has a mean of 80 and a standard deviation of 3. Assuming the distribution is bell-shaped and we randomly select a measurement:

a) What percentage of measurements are between 71 and 89?
b) What is the probability a person's blood systolic pressure measures more than 89?
c) What is the probability a person's blood systolic pressure being at most 75?
d) We should expect 15% of patients have a blood pressure below what measurement?
e) Would it be unusual for 3 patients to have a mean blood pressure measurement of more than 84? Explain.

Answer 1

Explained below.

Explanation:

Let X = systolic blood pressure measurements.

It is provided that,
`X\sim N(\mu=80,\sigma^(2)=3^(2))`.

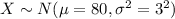(a)

Compute the percentage of measurements that are between 71 and 89 as follows:

`P(71<X<89)=P((71-80)/(3)<(X-\mu)/(\sigma)<(89-80)/(3))`

`=P(-3<Z<3)\\=P(Z<3)-P(Z<-3)\\=0.99865-0.00135\\=0.9973`

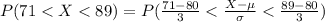
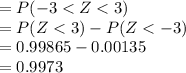
The percentage is, 0.9973 × 100 = 99.73%.

Thus, the percentage of measurements that are between 71 and 89 is 99.73%.

(b)

Compute the probability that a person's blood systolic pressure measures more than 89 as follows:

`P(X>89)=P((X-\mu)/(\sigma)>(89-80)/(3))`

`=P(Z>3)\\=1-P(Z<3)\\=1-0.99865\\=0.00135\\\approx 0.0014`

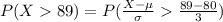
Thus, the probability that a person's blood systolic pressure measures more than 89 is 0.0014.

(c)

Compute the probability that a person's blood systolic pressure being at most 75 as follows:

Apply continuity correction:

`P(X\leq 75)=P(X<75-0.5)`

`=P(X<74.5)\\\\=P((X-\mu)/(\sigma)<(74.5-80)/(3))\\\\=P(Z<-1.83)\\\\=0.03362\\\\\approx 0.034`

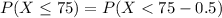
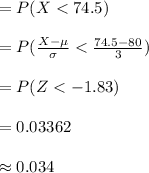
Thus, the probability that a person's blood systolic pressure being at most 75 is 0.034.

(d)

Let x be the blood pressure required.

Then,

P (X < x) = 0.15

⇒ P (Z < z) = 0.15

⇒ z = -1.04

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\\\-1.04=(x-80)/(3)\\\\x=80-(1.04*3)\\\\x=76.88\\\\x\approx 76.9`

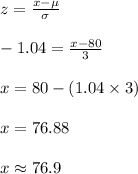
Thus, the 15% of patients are expected to have a blood pressure below 76.9.

(e)

A z-score more than 2 or less than -2 are considered as unusual.

Compute the z score for
`\bar x` as follows:

`z=(\bar x-\mu)/(\sigma/√(n))`

`=(84-80)/(3/√(3))\\\\=2.31`

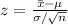
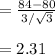
The z-score for the mean blood pressure measurement of 3 patients is more than 2.

Thus, it would be unusual.