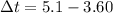Question

A 1.25-kg ball begins rolling from rest with constant angular acceleration down a hill. If it takes 3.60 s for it to make the first complete revolution, how long will it take to make the next complete revolution?

Answer 1

The time taken is
`\Delta t = 1.5 \ s`

Step-by-step explanation:

From the question we are told that

The mass of the ball is
`m = 1.25 \ kg`

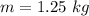
The time taken to make the first complete revolution is t= 3.60 s

The displacement of the first complete revolution is
`\theta = 1 rev = 2 \pi \ radian`

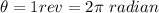
Generally the displacement for one complete revolution is mathematically represented as

`\theta = w_i t + (1)/(2) * \alpha * t^2`

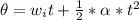
Now given that the stone started from rest
`w_i = 0 \ rad / s`

`2 \pi =0 + 0.5* \alpha *(3.60)^2`

`\alpha = 0.9698 \ s`

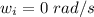
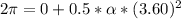
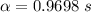
Now the displacement for two complete revolution is

`\theta_2 = 2 * 2\pi`

`\theta_2 = 4\pi`

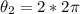
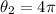
Generally the displacement for two complete revolution is mathematically represented as

`4 \pi = 0 + 0.5 * 0.9698 * t^2`

=>
`t^2 = 25.9187`

=>
`t= 5.1 \ s`

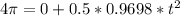
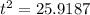
So

The time taken to complete the next oscillation is mathematically evaluated as

`\Delta t = t_2 - t`

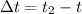
substituting values

`\Delta t = 5.1 - 3.60`

`\Delta t = 1.5 \ s`