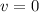Answer:
Step-by-step explanation:
dipole moment = qs = q x s
= charge x charge separation
charge = q
separation between charge = s
half separation l = s / 2
dipole has two charges + q and - q separated by distance s .
Potential at distance x along x axis due to + q
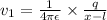
Potential at distance x along x axis due to - q

Total potential
v = v₁ + v₂
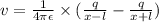
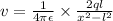
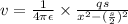
Potential at distance y along y axis due to + q
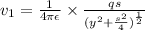
Potential at distance y along y axis due to - q
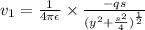
Total potential
v = v₁ + v₂