Answer:
The percentage change in resistance of the wire is 69%.
Step-by-step explanation:
Resistance of a wire can be determined by,
R = (ρl) ÷ A
Where R is its resistance, l is the length of the wire, A its cross sectional area and ρ its resistivity.
When the wire is stretched, its length and area changes but its volume and resistivity remains constant.
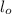 = 1.3l, and
= 1.3l, and
 =
=
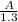
So that;
 = (ρ
= (ρ
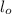 ) ÷
) ÷
 = (ρ × 1.3l) ÷ (
= (ρ × 1.3l) ÷ (
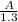 )
)
= (1.3lρ) ÷ (
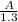 )
)
=
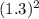 × [(ρl) ÷ A]
× [(ρl) ÷ A]
= 1.69R (∵ R = (ρl) ÷ A)
 = 1.69R
= 1.69R
Where
 is the new resistance,
is the new resistance,
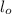 is the new length, and
is the new length, and
 is the new area after stretching the wire.
is the new area after stretching the wire.
The change in resistance of the wire =
 - R
- R
= 1.69R - 1R
= 0.69R
The percentage change in resistance =
 × 100
× 100
= 0.69 × 100
= 69%
The percentage change in resistance of the wire is 69%.