Question

A company would like to evaluate two incentive schemes that take effect once the worker exceeds standard performance. In the first case the benefits are split 30% to the worker and 70% to the company up to 120% performance. If the worker exceeds 120% performance, all of the earnings go to the worker. In the second case, all earnings beyond standard performance are split 50/50 between the worker and the company.

a. Plot the earnings for each scheme.
b. Derive the equations for worker earnings and normalized unit labor costs for each scheme
c. Find the point at which the two plans break even.
d. Which do you think would the company prefer?

Answer 1

B) plan 1 : worker earning y = x - 0.14 , unit labor =
`(x-(0.14))/(x)`

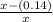
plan 2 : worker earning y = 0.5x + 0.5, unit labor = (0.5x + 0.5) / x

C) At 128%

D ) plan D IS PREFERABLE

Step-by-step explanation:

In the first case Benefits are split : 30% to worker , 70% to company ( up to 120% ) performance

In the second case benefits 50% go to the worker and 50% go the company

B) The equations for worker earnings and normalized unit labor costs for each scheme

Plan 1 :

y ( percentage earning of worker ) = 1

unit labor cost = Y / 1

y = 0 - 30

unit labor = 0.3 / x

y = x - 0.14 therefore unit labor =
`(x-(0.14))/(x)`

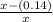
plan 2 :

y ( percentage earning of worker ) = 1, y = 0.5x + 0.5

unit labor cost : Y / 1 = (0.5x + 0.5) / x

C ) The point at which the two plans break even

0.5x + 0.5 = x - 0.14

0.5 + 0.14 = x - 0.5x

0.64 = x(1 - 0.5 )

x = 0.64 / 0.5 = 1.28 = 128%

D) The company would prefer plan 1