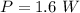Answer:
a
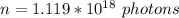
b
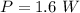
Step-by-step explanation:
From the question we are told that
The wavelength is
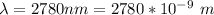
The energy is
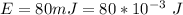
This energy is mathematically represented as
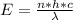
Where c is the speed of light with a value
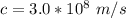
h is the Planck's constant with the value
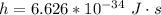
n is the number of pulses
So

substituting values
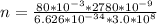
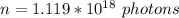
Given that the pulses where emitted 20 times in one second then the period of the pulse is
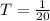
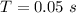
Hence the average power of photons in one 80-mJ pulse during 1 s is mathematically represented as
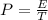
substituting values