Question

A hot metal bar is submerged in a large reservoir of water whose temperature is 60°F. The temperature of the bar 20 s after submersion is 120°F. After 1 min submerged, the temperature has cooled to 100°F. (Let y be measured in degrees Fahrenheit, and t be measured in seconds.) (a) Determine the cooling constant k. k = s−1 (b) What is the differential equation satisfied by the temperature y(t)? (Use y for y(t).) y'(t) = (c) What is the formula for y(t)? y(t) = (d) Determine the temperature of the bar at the moment it is submerged. (Round your answer to one decimal place.)

Answer 1

a. k = -0.01014 s⁻¹

b.
`\mathbf{(dy)/(dt) = - (In((3)/(2)))/(40)(y-60)}`

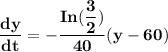
c.
`\mathbf{y(t) = 60+ (60 √(3))/(√(2)) \ e^{(-In((3)/(2))\ t)/(40)}}`

d. y(t) = 130.485°F

Explanation:

A hot metal bar is submerged in a large reservoir of water whose temperature is 60°F. The temperature of the bar 20 s after submersion is 120°F. After 1 min submerged, the temperature has cooled to 100°F.

(Let y be measured in degrees Fahrenheit, and t be measured in seconds.)

We are to determine :

a. Determine the cooling constant k. k = s−1

By applying the new law of cooling

`(dT)/(dt) = k \Delta T`

`(dT)/(dt) = k(T_1-T_2)`

`(dT)/(dt) = k (T - 60)`

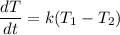
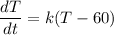
Taking the integral.

`\int (dT)/(T-60) = \int kdt`

㏑ (T -60) = kt + C

T - 60 =
`e^(kt+C)`

`T = 60+ C_1 e^(kt) ---- (1)`

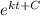
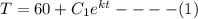
After 20 seconds, the temperature of the bar submersion is 120°F

T(20) = 120

From equation (1) ,replace t = 20s and T = 120

`120 = 60 + C_1 e^(20 \ k)`

`120 - 60 = C_1 e^(20 \ k)`

`60 = C_1 e^(20 \ k) --- (2)`

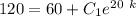
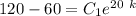
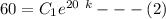
After 1 min i.e 60 sec , the temperature = 100

T(60) = 100

From equation (1) ; replace t = 60 s and T = 100

`100 = 60 + c_1 e^(60 \ t)`

`100 - 60 =c_1 e^(60 \ t)`

`40 =c_1 e^(60 \ t) --- (3)`

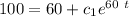
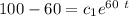
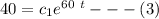
Dividing equation (2) by (3) , we have:

`(60)/(40) = (C_1e^(20 \ k ) )/(C_1 e^(60 \ k))`

`(3)/(2) = e^(-40 \ k)`

`-40 \ k = In ((3)/(2))`

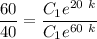
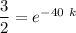
- 40 k = 0.4054651

`k = - (0.4054651)/( 40)`

k = -0.01014 s⁻¹

b. What is the differential equation satisfied by the temperature y(t)?

Recall that :

`(dT)/(dt) = k \Delta T`

`(dT)/(dt) = (- In ((3)/(2)))/(40)(T-60)`

Since y is the temperature of the body , then :

`\mathbf{(dy)/(dt) = - (In((3)/(2)))/(40)(y-60)}`

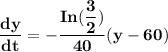
(c) What is the formula for y(t)?

From equation (1) ;

where;

`T = 60+ C_1 e^(kt) ---- (1)`

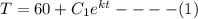
Let y be measured in degrees Fahrenheit

`y(t) = 60 + C_1 e^{-(In ((3)/(2)))/(40)t}`

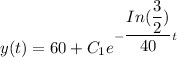
From equation (2)

`C_1 = \frac{60}{e^{20 * (-In((3)/(2)))/(40)}}`

`C_1 = \frac{60}{e^{-(1)/(2) {In((3)/(2))}}}`

`C_1 = \frac{60}{e^ {In((3)/(2))^(-1/2)}}}`

`C_1 = \frac{60}{\sqrt{(2)/(3)}}`

`C_1 = (60 * √(3))/(√(2))}`

`\mathbf{y(t) = 60+ (60 √(3))/(√(2)) \ e^{(-In((3)/(2))\ t)/(40)}}`

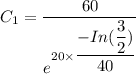
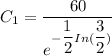
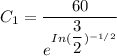
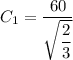
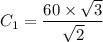
(d) Determine the temperature of the bar at the moment it is submerged.

At the moment it is submerged t = 0

`\mathbf{y(0) = 60+ (60 √(3))/(√(2)) \ e^{(-In((3)/(2))\ 0)/(40)}}`

`\mathbf{y(t) = 60+ (60 √(3))/(√(2)) }`

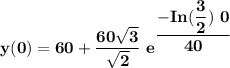
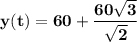
y(t) = 60 + 70.485

y(t) = 130.485°F