Question

A monopoly's cost function is

C = 1.5q^2 + 40 Q
and its the demand for its product is
p = 320-0.5Q
where Q is output, p is price, and C is the total cost of production. Determine the profit-maximizing price and output for a monopoly. The profit maximizing output level is units. (Enter a numeric response using an integer)

Answer 1

70 units

Step-by-step explanation:

The computation of profit maximizing output level is shown below:-

Monopolist perform Marginal Revenue which equivalent to the Marginal Cost as

MR = Marginal Revenue and MC = Marginal Cost

`MR = (\partial TR)/(\partial Q) = (\partial PQ)/(\partial Q) = (\partial (320-0.5Q)Q)/(\partial Q)`

`MR = (\partial (320Q -0.5Q^2))/(\partial Q)`

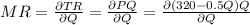
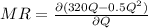
MR = 320 - Q

Now we will find the MC which is

`MC = (\partial TC)/(\partial Q) =(\partial (1.5Q^2 + 40Q))/(\partial Q) = 3Q + 40`

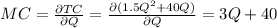
now we will put the value of which is into MR = MC

320 - Q = 3Q + 40

280 = 4Q

70 = Q

So, the profit maximizing output level is 70 units.