Question

A random sample of 12 second-year university students enrolled in a business statistics course was drawn. At the course's completion, each student was asked how many hours he or she spent doing homework in statistics. The data are listed below. 20, 29, 28, 22, 26, 22, 22, 18, 23, 21, 20, 27 It is known that the population standard deviation is 7. The instructor has recommended that students devote 2 hours per week for the duration of the 12-week semester, for a total of 24 hours. Test to determine whether there is evidence at the 0.07 significance level that the average student spent less than the recommended amount of time. Fill in the requested information below.A. The value of the standardized test statistic:Note: For the next part, your answer should use interval notation. An answer of the form (−[infinity],a) is expressed (-infty, a), an answer of the form (b,[infinity]) is expressed (b, infty), and an answer of the form (−[infinity],a)∪(b,[infinity]) is expressed (-infty, a)U(b, infty). B. The rejection region for the standardized test statistic:C. The p-value isD. Your decision for the hypothesis test: A. Reject H0. B. Do Not Reject H1. C. Do Not Reject H0. D. Reject H1.

Answer 1

Reject H₀.

Explanation:

In this case, we need to test whether the average student spent less than the recommended amount of time doing homework in statistics.

The provided data is:

S = {20, 29, 28, 22, 26, 22, 22, 18, 23, 21, 20, 27}

Compute the sample mean:

`\bar x=(1)/(n)\sum X=(1)/(12)\cdot [20+29+...+27]=23.167`

The population standard deviation is σ = 7.

The hypothesis for the test is:

H₀: The average student does not spent less than the recommended amount of time doing homework, i.e. μ ≥ 24.

Hₐ: The average student spent less than the recommended amount of time doing homework, i.e. μ < 24.

(A)

Compute the standardized test statistic value as follows:

`z=(\bar x-\mu)/(\sigma/√(n))`

`=(23.167-24)/(7/√(12))\\\\=-0.412`

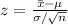
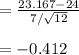
Thus, the standardized test statistic value is -0.412.

(B)

The significance level of the test is:

α = 0.07

The critical value of z is:

z₀.₀₇ = -1.476

The rejection region is:

(-∞, -0.1476)

(C)

Compute the p-value as follows:

`p-value=P(Z<-0.412)=0.34`

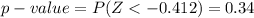
*Use a z-table.

Thus, the p-value is 0.34.

(D)

Since, p-value = 0.34 > α = 0.07, the null hypothesis was failed to be rejected at 7% level of significance.

Thus, the correct option is (A).