Question

A jetboat is drifting with a speed of 5.0\,\dfrac{\text m}{\text s}5.0 s m ​ 5, point, 0, start fraction, start text, m, end text, divided by, start text, s, end text, end fraction to the right when the driver turns on the motor. The boat speeds up for 6.0\,\text s6.0s6, point, 0, start text, s, end text with an acceleration of 4.0\,\dfrac{\text m}{\text s^2}4.0 s 2 m ​ 4, point, 0, start fraction, start text, m, end text, divided by, start text, s, end text, squared, end fraction leftward.

Answer 1

The question is incomplete. Here is the entire question.

A jetboat is drifting with a speed of 5.0m/s when the driver turns on the motor. The motor runs for 6.0s causing a constant leftward acceleration of magnitude 4.0m/s². What is the displacement of the boat over the 6.0 seconds time interval?

Answer: Δx = - 42m

Explanation: The jetboat is moving with an acceleration during the time interval, so it is a linear motion with constant acceleration.

For this "type" of motion, displacement (Δx) can be determined by:

`\Delta x = v_(i).t + (a)/(2).t^(2)`

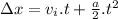
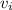`v_(i)` is the initial velocity

a is acceleration and can be positive or negative, according to the referential.

For Referential, let's assume rightward is positive.

Calculating displacement:

`\Delta x = 5(6) - (4)/(2).6^(2)`

`\Delta x = 30 - 2.36`

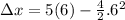
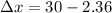
`\Delta x` = - 42

Displacement of the boat for t=6.0s interval is
`\Delta x` = - 42m, i.e., 42 m to the left.