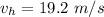Answer:
The velocity is
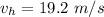
Step-by-step explanation:
From the question we are told that
The speed of the roller coaster at ground level is
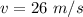
Generally we can define the roller coaster speed at ground level using the an equation of motion as
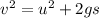
u is zero given that the roller coaster started from rest
So
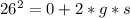
So
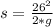
=>
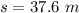
Now the displacement half way is mathematically represented as
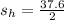
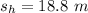
So
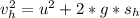
Where
 is the velocity at the half way point
is the velocity at the half way point
=>
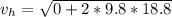
=>