Answer:
x = 300 feet
Explanation:
In the given right triangle,
Length of the string of the kite = 324 feet
Angle between the string and the ground = 68°
By applying law of Sines in the given right triangle,
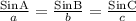
Now we substitute the values of angles and sides in the formula,

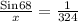
x = 324 × Sin(68)°
x = 300.41 feet
x ≈ 300 feet
Therefore, measure of side x = 300 feet will be the answer.