Question

A researcher is interested in finding a 95% confidence interval for the mean number of times per day that college students text. The study included 210 students who averaged 28 texts per day. The standard deviation was 21 texts.A. The sampling distribution follows a_______.1. "F"2. "normal"3. "T"4. "Chi-square" B. With 95% confidence the population mean number of texts per day of is between_______and______texts. A. 1. "24.92"2. "25.79"3. "27.37"4. "25.14"B. 1. "31.19"2. "31.20"3. "29.28"4. "30.86" C. If many groups of 210 randomly selected students are studied, then a different confidence interval would be produced from each group. About_______% of these confidence intervals will contain the true population mean number of texts per day and about______% will not contain the true population mean number of texts per day.A. 1. "5"2. "95"3. "1"4. "99"B. 1. "95"2. "99"3. "5"4. "1"

Answer 1

Answer: A. The sampling follows a normal distribution.

B. Between 25.14 and 30.86

C. About 95% will contain the true mean and about 5% won't

Explanation: A. The sampling is normally distributed because:

• it has a symmetric bell shape,
• mean and median are both the same and located at the center of graphic,

• approximately 68% of the data falls within one standard deviation;
• 95% falls within two standard deviations;
• 99.7% within 3 standard deviations;

B. For a 95% confidence interval: α/2 = 0.025

Since n = 210, use z-score = 1.96

To calculate the interval:

mean ±
`z.(s)/(√(n) )`

Replacing for the values given:

28 ±
`1.96.(21)/(√(210) )`

28 ±
`1.96*1.45`

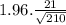
28 ± 2.84

lower limit: 28 - 2.84 = 25.14

upper limit: 28 + 2.84 = 30.86

Confidence Interval is between 25.14 and 30.86.

C. Confidence Interval at a certain percentage is an interval of values that contains the true mean with a percentage of confidence. In the case of number of times per day students text, 95% of the interval will contain the true mean, while 5% will not contain it.