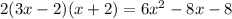Answer:
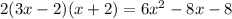
The factored form of
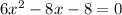 is
is
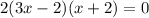
Explanation:
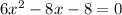
The way the quadratic equation was given, we can't have a factored form in the format:
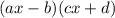
First, divide both sides by 2
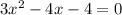
Now, it is about thinking. From the equation, we will get something in the format:
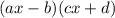
Let's expand this:

From here, we can give some values for those variables, based on the quadratic equation
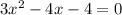 :
:
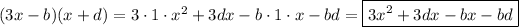
Once we want the middle term to be -4 and bd to be 4, we can easily evaluate the other variables.
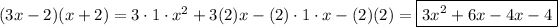
Therefore,

But we are not ready yet!
This is the factored form of
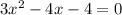 , to get the factored form of the problem equation, just multiply the factored form we got by 2.
, to get the factored form of the problem equation, just multiply the factored form we got by 2.