Question

An interference pattern is produced by light with a wavelength 590 nm from a distant source incident on two identical parallel slits separated by a distance (between centers) of 0.580 mm .

Required:

a. If the slits are very narrow, what would be the angular position of the first-order, two-slit, interference maxima?

b. What would be the angular position of the second-order, two-slit, interference maxima in this case?

Answer 1

a. 0.058°

b. 0.117°

Step-by-step explanation:

a. The angular position of the first-order is:

`d*sin(\theta) = m\lambda`

`\theta = arcsin((m \lambda)/(d)) = arcsin((1* 590 \cdot 10^(-9) m)/(0.580 \cdot 10^(-3) m)) = 0.058 ^(\circ)`

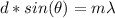
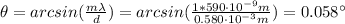
Hence, the angular position of the first-order, two-slit, interference maxima is 0.058°.

b. The angular position of the second-order is:

`\theta = arcsin((m \lambda)/(d)) = arcsin((2* 590 \cdot 10^(-9) m)/(0.580 \cdot 10^(-3) m)) = 0.12 ^(\circ)`

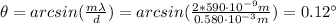
Therefore, the angular position of the second-order, two-slit, interference maxima is 0.117°.

I hope it helps you!