Answer:
(0.102, -0.062)
Explanation:
sample size in 2018 = n1 = 216
sample size in 2017 = n2 = 200
number of people who went for another degree in 2018 = x1 = 54
number of people who went for another degree in 2017 = x2 = 46
p1 = x1/n1 = 0.25
p2 = x2/n2 = 0.23
At 95% confidence level, z critical = 1.96
now we have to solve for the confidence interval =
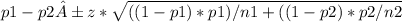
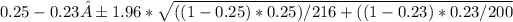
= 0.02 ± 1.96 * 0.042
= 0.02 + 0.082 = 0.102
= 0.02 - 0.082 = -0.062
There is 95% confidence that there is a difference that lies between - 0.062 and 0.102 on the proportion of students who continued their education in the years, 2017 and 2018.
There is no significant difference between the two.