Question

An engineer wishes to determine the width of a particular electronic component. If she knows that the standard deviation is 3.6 mm, how many of these components should she consider to be 90% sure of knowing the mean will be within ± 0.1 ±0.1 mm?

Answer 1

She must consider 3507 components to be 90% sure of knowing the mean will be within ± 0.1 mm.

Explanation:

We are given that an engineer wishes to determine the width of a particular electronic component. If she knows that the standard deviation is 3.6 mm.

And she considers to be 90% sure of knowing the mean will be within ±0.1 mm.

As we know that the margin of error is given by the following formula;

The margin of error =
`Z_(_(\alpha)/(2)_) * (\sigma)/(√(n) )`

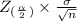
Here,
`\sigma` = standard deviation = 3.6 mm

n = sample size of components

`\alpha` = level of significance = 1 - 0.90 = 0.10 or 10%

`(\alpha)/(2) = (0.10)/(2)` = 0.05 or 5%

Now, the critical value of z at a 5% level of significance in the z table is given to us as 1.645.

So, the margin of error =
`Z_(_(\alpha)/(2)_) * (\sigma)/(√(n) )`

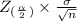
0.1 mm =
`1.645 * (3.6)/(√(n) )`

`√(n) = (3.6* 1.645)/(0.1 )`

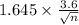
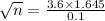
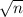`√(n)` = 59.22

n =
`59.22^(2)` = 3507.0084 ≈ 3507.

Hence, she must consider 3507 components to be 90% sure of knowing the mean will be within ± 0.1 mm.