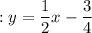Question

The equation of line WX is 2x + y = −5. What is the equation of a line perpendicular to line WX in slope-intercept form that contains point (−1, −2)?

Answer 1

Answer:
`y=\frac12x-(3)/(4)`

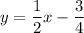
Explanation:

Given, The equation of line WX is 2x + y = −5.

It can be written as
`y=-2x-5` comparing it with slope-intercept form y=mx+c, where m is slope and c is y-intercept, we have

slope of WX = -2

Product of slopes of two perpendicular lines is -1.

So, (slope of WX) × (slope of perpendicular to WX)=-1

`-2*\text{slope of WX}=-1\\\\\Rightarrow\ \text{slope of WX}=(1)/(2)`

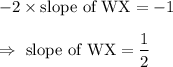
Equation of a line passes through (a,b) and has slope m:

`y-b=m(x-a)`

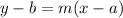
Equation of a line perpendicular to WX contains point (−1, −2) and has slope
`=\frac12`

`y-(-2)=(1)/(2)(x-(-1))\\\\\Rightarrow\ y+2=\frac12(x+1)\\\\\Rightarrow\ y+2=\frac12x+\frac12\\\\\Rightarrow\ y=\frac12x+\frac12-2\\\\\Rightarrow\ y=\frac12x-(3)/(4)`

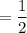
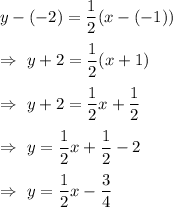
Equation of a line perpendicular to line WX in slope-intercept form that contains point (−1, −2)
`:y=\frac12x-(3)/(4)`