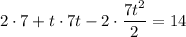Question

Consider the differential equation:

2y'' + ty' − 2y = 14, y(0) = y'(0) = 0.


In some instances, the Laplace transform can be used to solve linear differential equations with variable monomial coefficients.


If F(s) = ℒ{f(t)} and n = 1, 2, 3, . . . ,then

ℒ{tnf(t)} = (-1)^n d^n/ds^n F(s)


to reduce the given differential equation to a linear first-order DE in the transformed function Y(s) = ℒ{y(t)}.


Requried:

a. Sovle the first order DE for Y(s).

b. Find find y(t)= ℒ^-1 {Y(s)}

Answer 1

The first-order differential equation is solved by taking the Laplace transform of each term in the given differential equation and then solving for Y(s). Finally, the inverse Laplace transform is used to find y(t).

Step-by-step explanation:

To solve the given differential equation 2y'' + ty' - 2y = 14 using the Laplace transform, we first take the Laplace transform of each term.

• The Laplace transform of 2y'' is 2s2Y(s) - 2sy(0) - 2y'(0), which simplifies to 2s2Y(s) since y(0) = y'(0) = 0.
• The Laplace transform of ty' is -d/ds [sY(s)] using the property given.
• The Laplace transform of -2y is -2Y(s).
• The Laplace transform of 14 is 14/s.

Combining these, we get 2s2Y(s) - d/ds [sY(s)] - 2Y(s) = 14/s. This is the first-order linear differential equation in terms of Y(s), which we can solve for Y(s).

Upon solving this equation, we can then find y(t) by using the inverse Laplace transform ℑ-1 {Y(s)} to obtain the solution in the time domain.

Answer 2

(a) Take the Laplace transform of both sides:

`2y''(t)+ty'(t)-2y(t)=14`

`\implies 2(s^2Y(s)-sy(0)-y'(0))-(Y(s)+sY'(s))-2Y(s)=\frac{14}s`

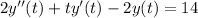
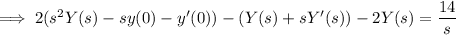
where the transform of
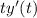`ty'(t)` comes from

`L[ty'(t)]=-(L[y'(t)])'=-(sY(s)-y(0))'=-Y(s)-sY'(s)`

This yields the linear ODE,

`-sY'(s)+(2s^2-3)Y(s)=\frac{14}s`

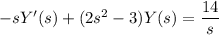
Divides both sides by
`-s`:

`Y'(s)+\frac{3-2s^2}sY(s)=-(14)/(s^2)`

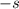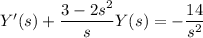
Find the integrating factor:

`\displaystyle\int\frac{3-2s^2}s\,\mathrm ds=3\ln|s|-s^2+C`

Multiply both sides of the ODE by
`e^(3\ln|s|-s^2)=s^3e^(-s^2)`:

`s^3e^(-s^2)Y'(s)+(3s^2-2s^4)e^(-s^2)Y(s)=-14se^(-s^2)`

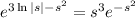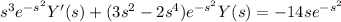
The left side condenses into the derivative of a product:

`\left(s^3e^(-s^2)Y(s)\right)'=-14se^(-s^2)`

Integrate both sides and solve for
`Y(s)`:

`s^3e^(-s^2)Y(s)=7e^(-s^2)+C`

`Y(s)=(7+Ce^(s^2))/(s^3)`

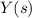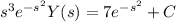
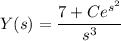
(b) Taking the inverse transform of both sides gives

`y(t)=\frac{7t^2}2+C\,L^(-1)\left[(e^(s^2))/(s^3)\right]`

I don't know whether the remaining inverse transform can be resolved, but using the principle of superposition, we know that
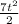`\frac{7t^2}2` is one solution to the original ODE.

`y(t)=\frac{7t^2}2\implies y'(t)=7t\implies y''(t)=7`

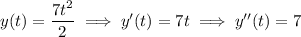
Substitute these into the ODE to see everything checks out:

`2\cdot7+t\cdot7t-2\cdot\frac{7t^2}2=14`