Question

Construct a polynomial function with the following properties: fifth degree, 4 is a zero of multiplicity 3, −2 is the only other zero, leading coefficient is 2.

Answer 1

`\Large \boxed{\sf \bf \ \ 2(x-4)^3(x+2)^2 \ \ }`

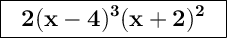
Explanation:

Hello, please consider the following.

Construct a polynomial function with the following properties...

... fifth degree

It means that the polynomial can be written as below.

`a_5x^5+a_4x^4+a_3x^3+a_2x^2+a_1x+a_0 \ \text{ with }a_5\text{ different from 0}\\\\\text{ or } k(x-x_1)(x-x_2)(x-x_3)(x-x_4)(x-x_5) \\\\ \text{ with k different from 0 and } (x_i)_(1\leqi\leq 5 ) \text { are the roots.}`

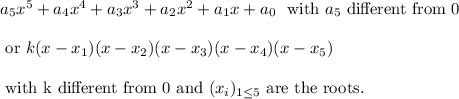
... 4 is a zero of multiplicity 3

We can write the polynomial as below.

`k(x-4)(x-4)(x-4)(x-x_4)(x-x_5)=k(x-4)^3(x-x_4)(x-x_5)`

... −2 is the only other zero

Because this is the only other zero, we can deduce that -2 is a zero of multiplicity 2.

`k(x-4)(x-4)(x-4)(x-x_4)(x-x_5)\\\\=k(x-4)^3(x-(-2))(x-(-2))\\\\=k(x-4)^3(x+2)^2`

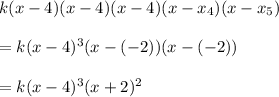
... leading coefficient is 2.

Finally, it means that k = 2 and then the polynomial function is:

`\large \boxed{2(x-4)^3(x+2)^2}`

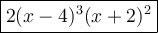
Hope this helps.

Do not hesitate if you need further explanation.

Thank you