Question

A thin metal plate, located in the xy-plane, has temperature T(x, y) at the point (x, y). Sketch some level curves (isothermals) if the temperature function is given by

T(x, y)= 100/1+x^2+2y^2

Answer 1

Explanation:

Given that:

`T(x,y) = (100)/(1+x^2+y^2)`

This implies that the level curves of a function(f) of two variables relates with the curves with equation f(x,y) = c

here c is the constant.

`c = (100)/(1+x^2+2y^2) \ \ \--- (1)`

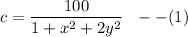
By cross multiply

`c({1+x^2+2y^2}) = 100`

`1+x^2+2y^2 = (100)/(c)`

`x^2+2y^2 = (100)/(c) - 1 \ \ -- (2)`

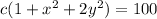
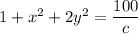
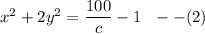
From (2); let assume that the values of c > 0 likewise c < 100, then the interval can be expressed as 0 < c <100.

Now,

`((x)^2)/((100)/(c)-1 ) + ((y)^2)/((50)/(c)-(1)/(2) )=1`

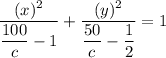
This is the equation for the family of the eclipses centred at (0,0) is :

`(x^2)/(a^2)+(y^2)/(b^2)=1`

`a^2 = (100)/(c) -1 \ \ and \ \ b^2 = (50)/(c)- (1)/(2)`

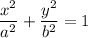
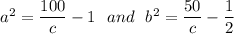
Therefore; the level of the curves are all the eclipses with the major axis:

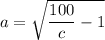`a = \sqrt{(100 )/(c)-1}` and a minor axis
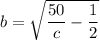`b = \sqrt{(50 )/(c)-(1)/(2)}` which satisfies the values for which 0< c < 100.

The sketch of the level curves can be see in the attached image below.