Question

Find secα, if sinα=−2/3 and 3π/2 <α<2π . Also the α=alpha symbol

Answer 1

Explanation:

Given sinα=−2/3, before we can get secα, we need to get the value of α first from sinα=−2/3.

`sin \alpha = -2/3`

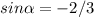
Taking the arcsin of both sides

`sin^(-1)(sin\alpha) = sin^(-1) -2/3\\ \\\alpha = sin^(-1) -2/3\\ \\\alpha = -41.8^0`

Since sin is negative in the 3rd and 4th quadrant. In the 3rd quadrant;

α = 180°+41.8°

α = 221.8° which is between the range 270°<α<360°

secα = sec 221.8°

secα = 1/cos 221.8

secα = 1.34