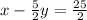Question

Fiona wrote the linear equation y = y equals StartFraction 2 over 5 EndFraction x minus 5.x – 5. When Henry wrote his equation, they discovered that his equation had all the same solutions as Fiona’s. Which equation could be Henry’s? x – x minus StartFraction 5 over 4 EndFraction y equals StartFraction 25 over 4 EndFraction.y = x – x minus StartFraction 5 over 2 EndFraction y equals StartFraction 25 over 4 EndFraction.y = x – x minus StartFraction 5 over 4 EndFraction y equals StartFraction 25 over 2 EndFraction.y = x – x minus StartFraction 5 over 2 EndFraction y equals StartFraction 25 over 2 EndFraction.y =

Answer 1

The 4th option

Explanation:

Answer 2

D.
`x-(5)/(2)y = (25)/(2)`

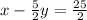
Explanation:

Given

`y = (2)/(5)x - 5`

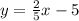
Required

Determine its equivalent

From the list of given options, the correct answer is

`x - (5)/(2)y = (25)/(2)`

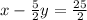
This is shown as follows;

`y = (2)/(5)x - 5`

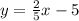
Multiply both sides by
`(5)/(2)`

`(5)/(2) * y = (5)/(2) * ((2)/(5)x - 5)`

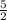
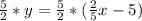
Open Bracket

`(5)/(2) * y = (5)/(2) * (2)/(5)x - (5)/(2) *5`

`(5)/(2)y = x - (25)/(2)`

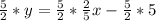
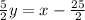
Subtract x from both sides

`(5)/(2)y - x = x -x - (25)/(2)`

`(5)/(2)y - x = - (25)/(2)`

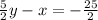
Multiply both sides by -1

`-1 * (5)/(2)y - x * -1 = - (25)/(2) * -1`

`-(5)/(2)y + x = (25)/(2)`

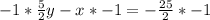
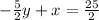
Reorder

`x-(5)/(2)y = (25)/(2)`

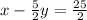
Hence, the correct option is D

`x-(5)/(2)y = (25)/(2)`